LeetCode 솔루션 분류
[1/11] 1443. Minimum Time to Collect All Apples in a Tree
본문
Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.
The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.
Example 1:
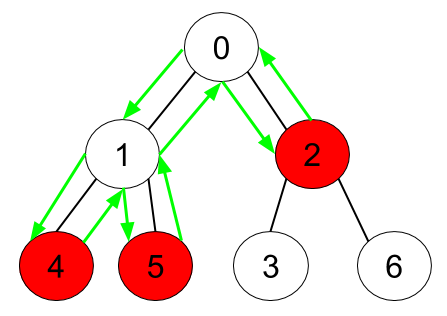
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false] Output: 8 Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
Example 2:
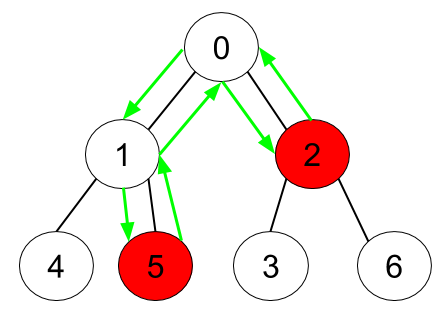
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false] Output: 6 Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
Example 3:
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false] Output: 0
Constraints:
1 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai < bi <= n - 1fromi < toihasApple.length == n
Accepted
89.9K
Submissions
142.7K
Acceptance Rate
63.0%
태그
#Facebook
관련자료
-
링크
댓글 1
학부유학생님의 댓글
- 익명
- 작성일
from collections import defaultdict
class Solution:
def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
graph = defaultdict(list)
for n1, n2 in edges:
graph[n1].append(n2)
graph[n2].append(n1)
need_visit = set()
def dfs(prev, curr):
res = False
for nxt in graph[curr]:
if nxt == prev: continue
temp = dfs(curr, nxt)
res = res or temp
res = res or hasApple[curr]
if res: need_visit.add(curr)
return res
dfs(-1,0)
return max(2*len(need_visit) - 2,0)










